KAUNO TECHNOLOGIJOS UNIVERSITETAS
Signalų apdorojimo katedra
Dažninės grandinių charakteristikos
„Grandinių teorija 2“ semestro darbo 1 dalis
Studentas: Ernestas Šeputis, RR-3/2 gr.
parašas, data
Dėstytojas: Olgirdas Tumšys
Kaunas, 2014
Darbo savarankiškumo patvirtinimo puslapis
| Mokomasis dalykas: | T190B263 – Grandinių teorija 2 | |
| Darbo kategorija: | Semestro darbas | |
| Semestras: | 2014 m. ruduo | |
| Akad. grupė | ||
| Studentas: | Studento bilieto numeris: |
| Patvirtinimas parašuAš patvirtinu, kad esu asmeniškai atsakingas už šį darbą. Aš atlikau šį darbą visai savarankiškai: jokių šio darbo dalių nekopijavau arba negavau iš kitų asmenų. Aš suprantu, kad bet koks mano sukčiavimas yra nesuderinamas su akademinės etikos normomis, su KTU studento moralės ir etikos kodeksu.
……………………. …………………………….. Data: Vardas, pavardė |
| Dėstytojo išvada
………………………. Data |
Darbo tikslas – apskaičiuoti tiriamos grandinės (dvipolio ir keturpolio) grandinės funkcijas, nubraižyti jų amplitudės ir fazės dažnines charakteristikas.
1. Sudaroma grandinė ir nubraižoma jos schema.
KTU akademinės informacinės sistemos vidinis kodas: A9429.
Varianto numeris: 42. Varianto numerį atitinkantis kodas: 2461359.
Grafo numeris: 9.
Sudaromos grandinės grafas M pavaizduotas 1 pav.

1 pav. Sudaromos grandinės grafas
Kodas grandinės schemai sudaryti: 2461359
Pirmasis ir antrasis varianto kodo skaitmenys 2 ir 4 – tai numeriai grafo šakų, kuriose įjungti varžiniai elementai.
Trečiasis ir ketvirtasis varianto kodo skaitmenys 6 ir 1 – tai numeriai grafo šakų, kuriose įjungti induktyvieji elementai.
Penktasis ir šeštasis kodo skaitmenys 3 ir 5 – numeriai grafo šakų, kuriose įjungti talpiniai elementai.
Septintasis kodo skaitmuo – tai numeris šakos, kurioje yra kintamasis varžinis elementas.
Septintasis kodo skaitmuo taip pat yra ir koeficientas K grandinės elementų parametrų skaičiavimui (jeigu septintasis kodo skaitmuo lygus 0, K=10).
Pirmasis grafo mazgas laikomas įėjimo mazgu, o ketvirtasis – bendruoju (nuliniu) mazgu.
Visų kitų grandinės, atitinkančios nurodytą grafą, šakų nėra.
Sudaryta grandinės schema parodyta 2 pav.
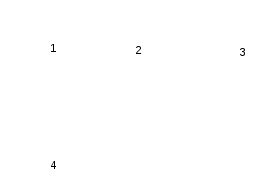
2 pav. Sudaryta grandinės schema
Grandinės schema pertvarkoma, kairėje pusėje išvedant 1 ir 4 mazgus (grandinės įėjimą), o dešinėje – 3 ir 4 mazgus (grandinės išėjimą). Pertvarkyta grandinės schema pateikta 3 pav.
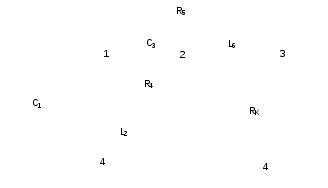
3 pav. Pertvarkyta grandinės schema su sužymėtais grandinės elementais
2. Sunumeruojami schemos elementai (3 pav.). Parametrai apskaičiuojami iš tokių lygčių:
K=9.
R4=0,2∙R5=K/2∙3 kΩ=9/2∙3=13.5 kΩ;
R4=13.5 kΩ;
0,2∙R2=13.5 kΩ;
R5=13500/0,2=6.75 kΩ.
L2=2∙L6=K/2∙3 mH=9/2∙3=13.5 mH;
L2=13.5 mH;
2∙L6=13.5 mH;
L6=13.5/2=6.75 mH.
C1=2∙C3=K/2∙6 nF=9/2∙6=27 nF;
C1=27 nF;
2∙C3=27 nF;
C3=27/2=13.5 nF.
RK=K/2∙3 kΩ=9/2∙3=13.5 kΩ.
Grandinės elementų parametrai surašomi grandinės schemoje (4 pav.)
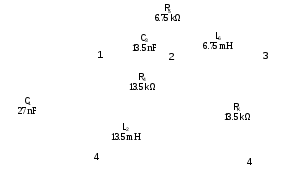
4 pav. Grandinės schema su elementų parametrais
3. Dvipolio analizė
Sudaryta grandinė tarp pirmojo ir ketvirtojo mazgų tiriama kaip dvipolis (5 pav.). Apskaičiuosime šio dvipolio įėjimo impedanso kompleksines dažnines charakteristikas.
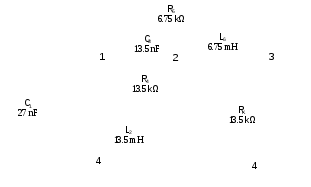
5 pav. Grandinės schema su elementų parametrais
Užrašomi grandinės elementų impedansai:
![]()
![]()
![]()
![]()
![]()
![]()
Grandinės schema su surašytais grandinės elementų impedansais pateikta 6 pav.
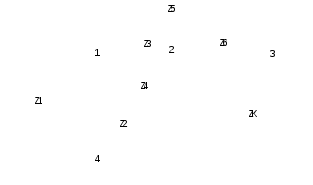
6 pav. Grandinės schema su impedansais
Grandinės įėjimo impedanso skaičiavimas atliekant grandinės ekvivalenčiuosius pakeitimus.
Sujungiami lygiagrečiai sujungti impedansai Z1 ir Z2, Z3 ir Z4:


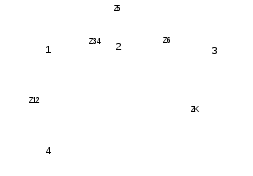
7 pav. Supaprastinta grandinės schema
Sujungiami lygiagrečiai sujungti impedansai Z12 ir Z34, Z6 ir ZK:


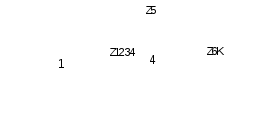
8 pav. Supaprastinta grandinės schema
Sujungiami nuosekliai sujungti impedansai Z5 ir Z6K, ir sujungiami lygiagrečiai sujungti impedansai Z1234 ir Z56K. Grandinės įėjimo impedansas:

Įėjimo impedanso amplitudės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 9 pav.
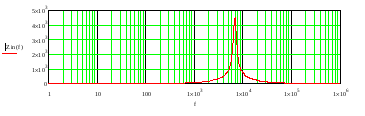
9 pav. Įėjimo impedanso amplitudės dažninė charakteristika
Impedanso fazės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 10 pav.
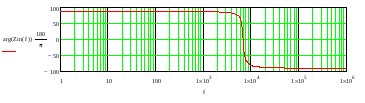
10 pav. Įėjimo impedanso fazės dažninė charakteristika
Grandinės įėjimo impedanso skaičiavimas matricų metodu
Sudarome grandinės (6 pav.) admitansų matricą:

Tuomet grandinės įėjimo impedansas Zin:
Z=∆11/∆
Čia ∆11 yra admitansų matricos 11 adjunktas, o yra admitansų matricos determinantas.
Įėjimo impedanso amplitudės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 11 pav.
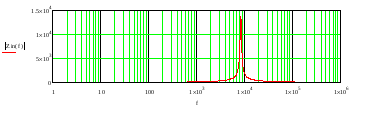
11 pav. Įėjimo impedanso amplitudės dažninė charakteristika
Impedanso fazės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 12 pav.
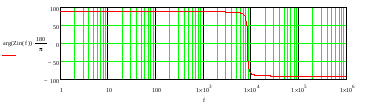
12 pav. Įėjimo impedanso fazės dažninė charakteristika
Grandinės įėjimo impedanso skaičiavimas keturpolių metodu
Grandinė išskaidoma į elementariuosius keturpolius (13 pav.)

13 pav. Grandinės išskaidymas į elementariuosius keturpolius
Naudojantis literatūroje pateikiamomis lentelėmis, užrašomi elementariųjų keturpolių parametrai.


![]()
![]()
![]()
Lygiagrečiai sujungti keturpoliai A4 ir A2 keičiami keturpoliu A24 (14 pav.), keturpolių A parametrus verčiant į keturpolių Y parametrus ir juos sudedant.
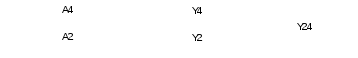
14 pav. Keturpolių A4 ir A2 pakeitimas į keturpolį Y24


![]()
Tuomet keturpolio Y parametrai paverčiami į keturpolio A parametrus.

Pakopiškai sujungtus keturpolius A24 ir A3 pakeičiame vienu keturpoliu A234 (15 pav.):

15 pav. Keturpolių A24 ir A3 pakeitimas į keturpolį A234
![]()
Lygiagrečiai sujungti keturpoliai A234 ir A5 keičiami keturpoliu A2345 (16 pav.), keturpolių A parametrus verčiant į keturpolių Y parametrus ir juos sudedant.
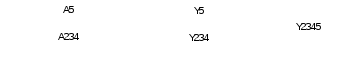
16 pav. Keturpolių A234 ir A5 pakeitimas į keturpolį Y2345


![]()
Tuomet keturpolio Y parametrai paverčiami į keturpolio A parametrus.

Pakopiškai sujungtus keturpolius A2345 ir A1 pakeičiame vienu keturpoliu A (17 pav.):
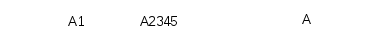
17 pav. Keturpolių A1 ir A2345 pakeitimas į keturpolį A
![]()
Galime surasti jo įėjimo impedansą:

Įėjimo impedanso amplitudės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 18 pav.

18 pav. Įėjimo impedanso amplitudės dažninė charakteristika
Impedanso fazės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 19 pav.
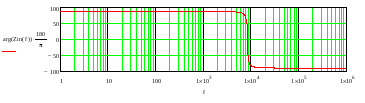
19 pav. Įėjimo impedanso fazės dažninė charakteristika
4. Keturpolio analizė
Sudarytos grandinės įėjimu laikant pirmąjį ir ketvirtąjį mazgus, o išėjimu – trečiąjį ir ketvirtąjį mazgus, toliau grandinę tirsime kaip keturpolį (20 pav.). Apskaičiuosime šio keturpolio įtampos perdavimo funkcijos kompleksines dažnines charakteristikas.
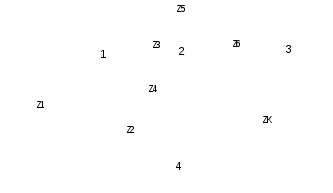
20 pav. Sudaryta keturpolio grandinė
Grandinės įtampos perdavimo funkcijos skaičiavimas matricų metodu
Naudojant grandinės admitansų matricą:

grandinės įtampos perdavimo funkcija H bus lygi atviro keturpolio įtampos perdavimo funkcijai:
H=∆13/∆11
Čia yra admitansų matricos 11 adjunktas, o yra admitansų matricos 13 adjunktas.
Įtampos perdavimo funkcijos amplitudės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 21 pav.
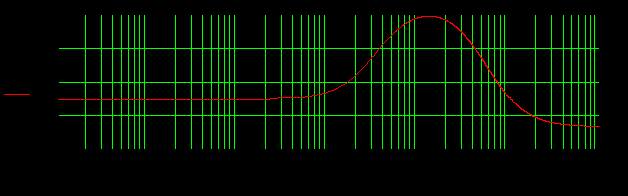
21 pav. Įtampos perdavimo funkcijos amplitudės dažninė charakteristika
Įtampos perdavimo funkcijos fazės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 22 pav.
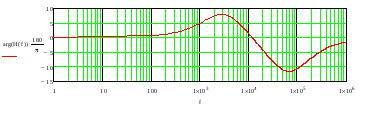
22 pav. Įtampos perdavimo funkcijos fazės dažninė charakteristika
Grandinės įtampos perdavimo funkcijos skaičiavimas keturpolių metodu
Turint grandinės keturpolio A parametrus A (17 pav.), įtampos perdavimo funkcija bus:
![]()
Įtampos perdavimo funkcijos amplitudės dažninė charakteristika dažnių intervale 1 Hz – 1 MHz pateikta 23 pav.
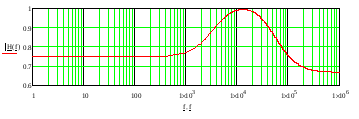
23 pav. Įtampos perdavimo funkcijos amplitudės dažninė charakteristika
Įtampos perdavimo funkcijos fazės dažninė charakteristika dažnių intervale 1Hz – 1 MHz pateikta 24 pav.
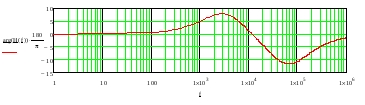
24 pav. Įtampos perdavimo funkcijos fazės dažninė charakteristika
5. Grandinės modeliavimas kompiuterinės grandinių analizės priemonėmis
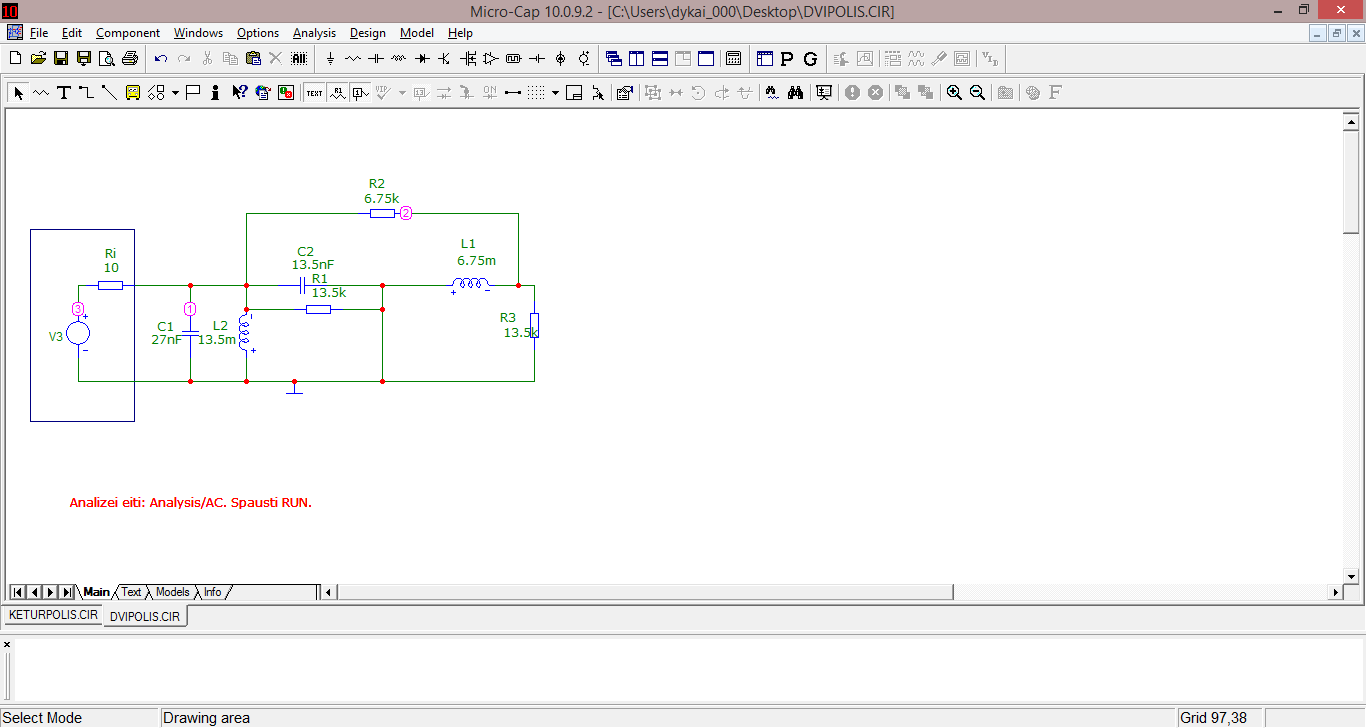
25 pav. Grandinės schema Micro-Cap programoje
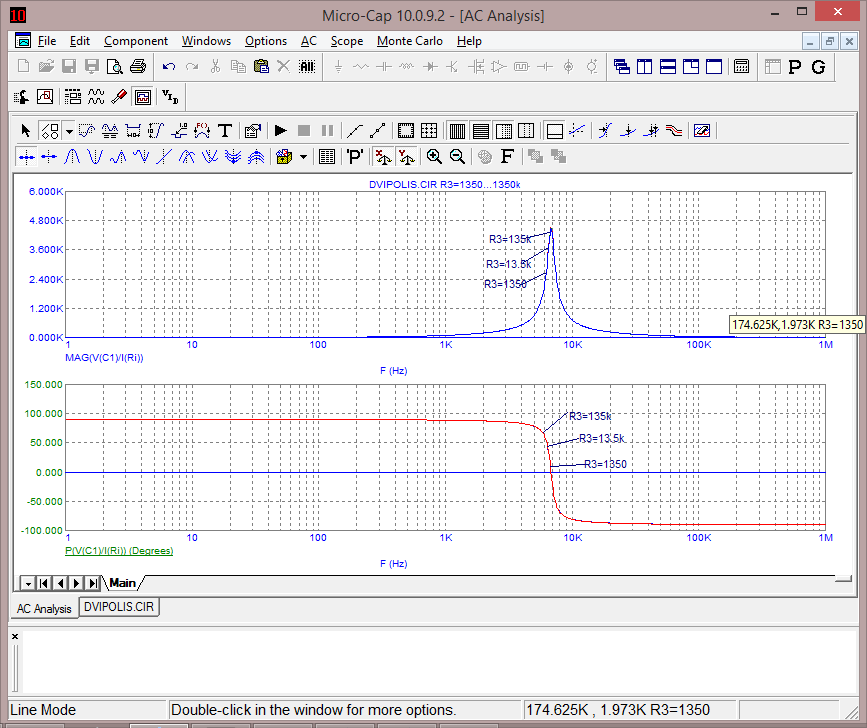
26 pav. Įėjimo impedanso amplitudės ir fazės dažninės charakteristikos keičiant R3 elemento varžą
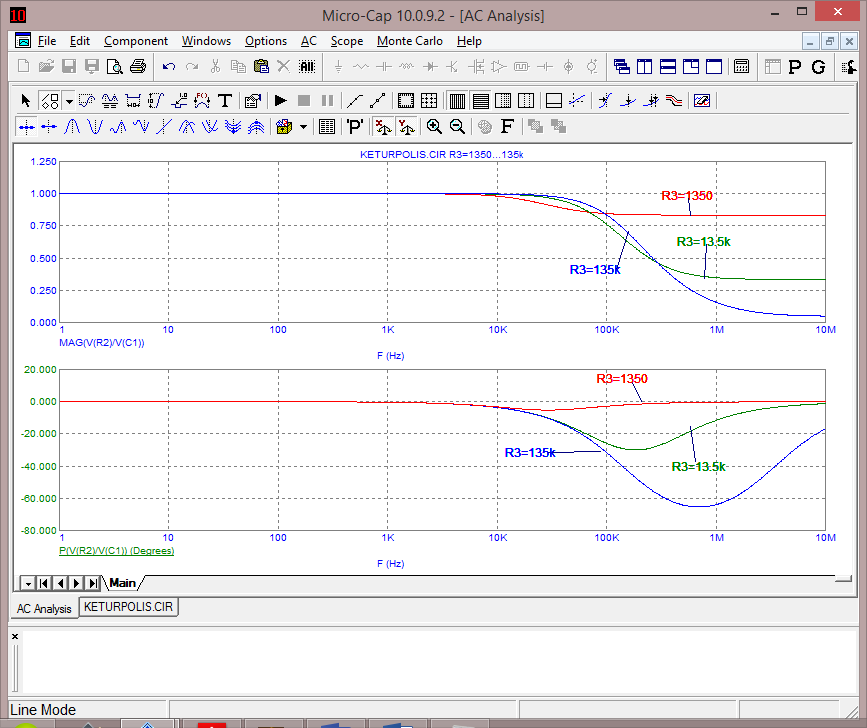
27 pav. Įtampos perdavimo funkcijos amplitudės ir fazės dažninės charakteristikos keičiant R3 elemento varžą
Išvados
Atlikęs darbą išmokau tirti dvipolius ir keturpolius – apskaičiuoti tiriamos jų funkcijas, nubraižyti jų amplitudės ir fazės dažnines charakteristikas.